1.3 Statistik und Verteilung
Warum Statistik:
Die Beurteilung der Qualität jedes einzelnen Produktes eines Prozesses ist nicht durchführbar und / oder zu teuer. Wesentlich wirtschaftlicher ist es, eine Stichprobe des Produktes zu beurteilen und die Ergebnisse für eine Voraussage über die Gesamtheit aller gefertigten Produkte zu verwenden. Mit statistischen Verfahren kann man Aussagen über die Qualität des Produktes machen.
Vertrauensniveau der Voraussagen:
Die Genauigkeit der Voraussagen läßt sich abhängig von dem Stichprobenumfang und von den verwendeten Methoden abschätzen.
Mehrere Verfahren zur Analyse von Daten:
Es gibt mehrere Verfahren zur Analyse von Daten. Richtig angewendet führen diese statistischen Verfahren zu Voraussagen mit einem hohen Grad an Genauigkeit.
Statistische Verfahren:
a) tabellarische Auflistung:
1. 25,13
2. 25,11
3. 25,11
4. 25,10
5. 25,14
.
.
.
50. 25,12
2. 25,11
3. 25,11
4. 25,10
5. 25,14
.
.
.
50. 25,12
b) Strichliste:
c) Histogramm:
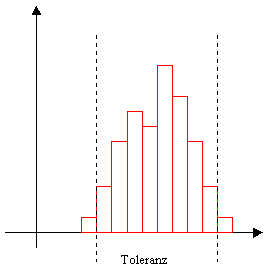
Ein Histogramm ergibt ein deutliches Bild des Prozesses über die Streuung hinsichtlich:
- Positionierung
- Form
- Größe
d) Stetige Verteilungen:
Das Histogramm ergibt die Verteilungskurve bzw. Verteilungsfunktion nach Verbindung der höchsten Punkte der Säule:
 |
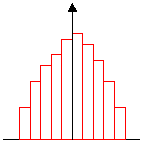Verteilung der 50-Teile Stichprobe |
 |
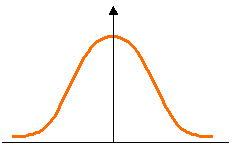Verteilung der Grundgesamtheit |
Es gibt viele Arten von Verteilungen.
Diese Arten von Verteilung können beschreiben werden durch Modelle. Die Verteilungen oder das Verteilungsmodell, das man in der Natur oder bei Fertigungsprozessen am häufigsten begegnet ist die Normal- oder Gauß´sche Verteilung. Jedes Modell kann mit Hilfe einer Verteilungsfunktion beschreiben werden. Jede Verteilung wird durch Kennwerte beschreiben.
Somit gibt z.B. für eine Normalverteilung.
Somit gibt z.B. für eine Normalverteilung.
Verteilungen können sich unterscheiden in:
- Form:
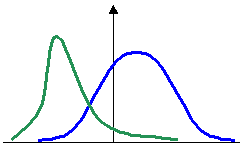
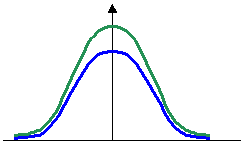
- Streuung:
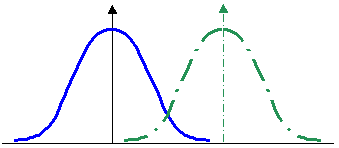
- Lage:
- Streuung:
- Lage:
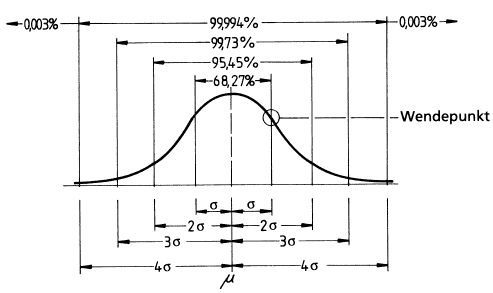
Prozentsätze der Normalverteilung
Wenn Mittelpunkt und Standardabweichung bekannt sind, ist es möglich mit angemessener Genauigkeit den Anteil der Grundgesamtheit vorauszusagen, der zwischen zwei Grenzwerte fällt.
Normalverteilung:
Die Normalverteilung ist graphisch eine symetrische Glockenkurve. Für die Stichprobe ist sie durch zwei Kennwerte bestimmt.
Der Mittelwert: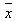
(genannt: x quer)
Der Mittelwert ist ein Maß für die Lage der Verteilung der Stichprobe:
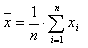
Die Standardabweichung "s" ist ein Maß für die Streuung des Prozesses.
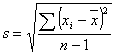
Die Standardabweichung "s" ist der Abstand zwischen Mittelwert und Wendepunkt der Glockenkurve.
Der Mittelwert:
(genannt: x quer)Der Mittelwert ist ein Maß für die Lage der Verteilung der Stichprobe:
Die Standardabweichung "s" ist ein Maß für die Streuung des Prozesses.
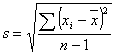
Die Standardabweichung "s" ist der Abstand zwischen Mittelwert und Wendepunkt der Glockenkurve.