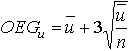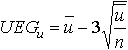1.4.2 Attributive Regelkarten
Attributive Regelkarten basieren auf dem Vorhandensein und Entdecken von Fehlern (Gut / Schlecht-Prinzip; zählende Prüfung
Variable Prüfung: Anzeige der Größe und Richtung der Streuung
Attributive Prüfung:
- Anzeige des Anteils und der Streuung der fehlerhaften Produkte
- erfordert große Stichprobenumfänge
- setzt häufig Fehler voraus
- Einsatz wo messen nicht praktikabel ist
- braucht, klar definierte Fehlerkriterien
Notwendige Schritte zur Aufstellung von Fehlerkriterien:
- Erstelle Qualitätsstandard
- Entwickle für die Aufgabe geeignete visuelle Hilfen
- Erkläre die Standards den betroffenen Mitarbeitern
- Mitarbeiter sollen fähig sein, die Standards zu unterscheiden z.B. gutes Sehvermögen
- Schule fehlerentdeckende Fertigkeiten und Urteilsvermögen
- Einwandfreie Prüfumgebung (z.B. Temp., Luftfeuchtigkeit)
- Mögliche Regelkarten
| p-Karte: | Anteil fehlerhafter Einheiten (Stichprobenumfang nicht konstant) |
| np-Karte: | Anzahl fehlerhafter Einheiten (Stichprobenumfang ist konstant) |
| c-Karte: | Anzahl Fehler (von Stichproben mit konstantem Umfang) |
| u-Karte: | Anteil Fehler pro Einheit (von Stichprobenwechselnder Größe) |
Beispiel von Fällen, in denen Karten angewandt werden können
| Merkmale | Regelkarte |
|---|---|
| Vorhandensein / Nichvorhandensein erforderlicher Schrauben Elektrischer Strom fließt / fließt nicht Wellendurchmesser richtig / falsch |
p-Karte für Anteil fehlerhafter Einheiten oder
np-Karte für die Anzahl fehlerhafter Einheiten (Stichproben gleichen Umfangs) |
| Blasen in einer Windschutzscheibe Farbfehler an einer Tür Längsrisse im Material |
c-Karte für die Anzahl Fehler (Stichproben gleichen Umfangs) oder
u-Karte für die Anzahl Fehler pro untersuchter Einheit |
Die p-Karte:
Beispiel p-Regelkarte mit Prozessverbesserung
wichtig:
| a) | gut / schlecht Prinzip | |
| b) | Anteil: |  |
Datensammlung:
- groß (>50)
- mehrere fehlerhafte Teile in einer Stichprobe
- empfehlenswert: Stichprobenumfang möglichst konstant halten
- geeignete Maßstabauswahl
Berechnung der Eingriffgrenzen:
Berechne für den Untersuchungszeitraum den mittleren Anteil fehlerhafter Einheiten.
Berechnen des durchschnittlichen Probenumfang:Obere und Untere-Eingriffgrenze: |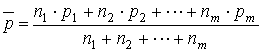
n = Stichprobengröße p = Fehler m = Stichprobenanzahl  = Anzahl fehlerhafter Anteile in der R-ten Stichprobe der Größe  |
 |
= wechselnde Anzahl geprüfter Einheiten |
  |
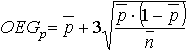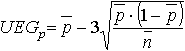Stichprobenumfang soll nicht mehr als 25% schwanken |
Analyse der Datenpunkte:
- Punkte außerhalb der Eingriffgrenzen:
Oberhalb der OEG:- Prozeßgüte verschlechtert
- Punkt falsch eingezeichnet
- Eingriffgrenze falsch
- Bewertungskriterium verschärft (Prüfer, Lehre)
Unterhalb der UEG:- Eingriffgrenze falsch
- Punkt falsch eingezeichnet
- Prozeßgüte ist verbessert
- spezielle Kurvenverläufe innerhalb der Eingriffsgrenzen und nicht zufällige Kurvenverläufe.
Prozeß- bzw. Systemänderungen:
nach Beseitigung von systematischen Fehlern muß der Mittelwert und die Eingriffgrenzen neu berechnet werden.
Die np-Karte:
Anzahl fehlerhafter Einheiten in einer Stichprobe
Stichprobenumfang ist konstant
Anzahl fehlerhafter Einheiten einfacher zu berechnen als Anteil
Berechnung der Eingriffgrenzen:
 |
 = Anzahl fehlerhafter Einheiten in der Stichprobe 1,2,... |
 |
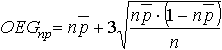n = Stichprobenumfang |
 |
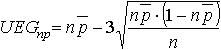m = Anzahl der Stichproben |
Beispiel
| In der ersten Probe von Erdnüssen (n = 100) sind 3 Erdnüsse |  |
schlecht ! |
Die c-Karte:
Bei der c-Karte wird die Anzahl der Fehler in einer Stichprobe gezählt (Im Gegensatz zu der Anzahl fehlerhafter Einheiten auf einer np-Karte). Die c-Karte erfordert einen konstante Menge Prüfmaterial.
Anwendung:
- Wenn die Teile über einen mehr oder weniger kontinuierlichen Produktionsfluß verstreut sind, z.B.:
- Risse über die Länge eines Stabes
- Blasen im Glas
- Stellen dünner Isolation auf einem Draht
- wenn die Fehler in einer untersuchten Stichprobe von vielen verschiedenen Ursachen stammen könnten, z.B.:
- Aufzeichnung einer Reparaturstation, in der jedes einzelne Fahrzeug oder Teil einen oder mehrere Fehler der verschiedensten Art haben könnte.
Berechnung der Eingriffgrenze:
| Durchschnittliche Fehlerzahl: |  |
m = Stichprobenanzahl |
Die u-Karte:
Anwendung:
Wenn die Fehler pro Einheit in einer Stichprobe gezählt werden. Der Stichprobenumfang braucht nicht konstant zu sein.
| Fehlerzahl pro Einheit: |  |
Prozeßmittelwert für die Fehlerzahl pro Einheit:
 |
 |
Eingriffsgrenzen:
