1.4 Die Regelkarte
1.4.1 Prozeßführung:
Ein Prozeß ist "statistisch unter Kontrolle", und somit voraussagbar hinsichtlich:
- Qualität
- Produktivität
- Kosten
Prozeßregelkarten:
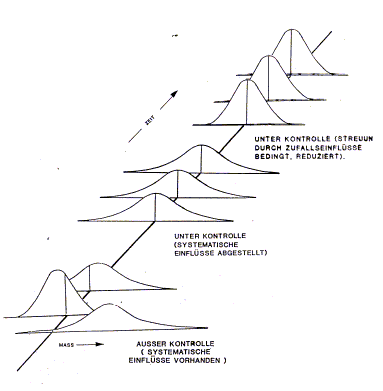
Aufgaben der Prozeßregelkarten:
- zu verdeutlichen, ob sich der Prozeß unter statistischer Kontrolle befindet bzw. das Vorhandensein von systematischen Einflüssen zu signalisieren
- den Zustand "unter statistischer Kontrolle" zu halten
- Maßnahmen am Prozeß zur Verbesserung der Fähigkeit nachzuweisen
Kontinuierliche Vorgehensweise:
- Datensammlung
- Prozeßregelung
- Fähigkeitsverbesserung
- Datensammlung:
Zwei Arten von Daten
-
Variable Daten (messende Prüfung)
Die Beurteilung der Ausführungsqualität erfolgt bei der variablen Prüfung aufgrund der Messergebnisse oder nach Kennzahlen die aus den Meßergebnissen berechnet werden. -
Attributive Daten (zählende Prüfung)
Die Beurteilung der Ausführungsqualität nach dem gut/schlecht - Prinzip
Beispiel von Daten
- Meßwerte eines Werkstückes
- Anzahl Lackläufer auf einer Tür
- Fahrzeugdurchlaufzeiten
- Buchführungsfehler
Diese Daten werden in eine graphische Form gebracht.
-
-
Regeln:
Berechnung der Eingriffgrenzen
Eingriffgrenzen sind keine Spezifikationsgrenzen oder Zielvorstellungen, sondern ein Spiegelbild der natürlichen Prozeßsteuerung.Durch Vergleich der Daten mit den Eingriffgrenzen wird festgestellt, ob die Streuung stabil ist und nur durch Zufallseinflüsse verursacht wird.
Liegen systematische Fehler vor:
- Ursachenfindung
- Ergreifen von Maßnahmen
Liegen keine systematische Fehler vor, dann folgt: die Fähigkeitsverbesserung.
-
Fähigkeitsverbesserung:
Feststellen ob ein Prozeß fähig ist, d.h. kann man mit der Streuung der Daten (ohne systemetische Fehler) leben.
Wenn nicht, dann muß das System verbessert werden (neue Maschinen, Klimaanlagen etc.) oder 100%-ige Kontrolle.
Nutzen von Regelkarten:
- Einfaches Mittel zur Prozeßregelung
- Voraussage der Qualität des Produktes, welcher durch den stabilen Prozeß unter statistischen Kontrolle gefertigt wird.
Dies hat zur Folge:- Erhöhung des Anteils der Produkte, die die Erwartungen des Abnehmers erfüllen
- Reduzierung von Ausschuß oder Nacharbeit
- Erhöhung der (Effektivität) effektiven Kapazität
- Gemeinsame Diskussionsbasis über Güte eines Prozesses, im Betrieb bzw. zwischen Lieferant, Kunde und Erzeuger
- keine fehlgeleiteten Problemslösungsbemühungen
Vorbereitung zur Einführung:
- Schaffung des Arbeitsumfeldes
- ausreichende Qualifikation des Mitarbeiters
- Qualitätsgedanken geht vor Quantitätsgedanke (Aushängen der Reklamationsrate etc.)
- Förderung von Verbesserungsmaßnahmen
- Verstehen des (Fertigungs-) Prozesses
- Bestimmung der Qualitätsmerkmale
- Definition des Meßsystems
- Reduzierung unnötiger Streuung z.B. bekanntes Eingangsmaterial verwenden
Bei der Auswahl vom Meßsystem und von den Merkmale sollen noch folgende Punkte beachtet werden:
- Bedürfnisse des Arbeitnehmers
- Vorhanden sein und mögliche Problembereiche definieren
- Korrelation der Meßdaten
Das Meßinstrument:
Die verschiedenen Karten
- Anzahl fehlerhafter Einheiten
- Anzahl von Fehlern Urwert
- Mittelwert
- Median
- Standardabweichung
- Spannweite
- oder andere Merkmale
Prozeßparameter müssen bekannt sein
Unterschiede zwischen Europa und USA
Unterschied ist jedoch, die Lage der Eingriffsgrenzen:
Eingriffsgrenzen sind keine Toleranzgrenzen Die Obere- und Untere-Eingriffsgrenze (OEG und UEG) ist eine Grenze bei deren Über- oder Unterschreitung eine Korrektur des Prozesses oder Klärung der Ursache erfolgen muß.
Diese Grenze wir nur nach statistischen Kriterien festgelegt. Ein Kriterium ist die statistische Sicherheit.
Obere- und Untere-Eingriffgrenze
Irrtumswahrscheinlichkeit (a):
Regelkarte mit systematischer Mittelwertänderung
 /R-Karte:
/R-Karte:
Wahl, Häufigkeit und Anzahl der Stichproben:
Die Stichprobe sollte so gewählt werden, daß:
- die Streuung zwischen den Teilen innerhalb einer Probe klein ist.
- Streuung jedoch noch sichtbar ist, damit Abweichungen zwischen den verschiedenen Stichprobenaufnahmen noch interpretierbar sind.
Die Häufigkeit sollte so gewählt werden, daß Änderungen des Prozesses (Schichtwechsel, Materiallose, ect.) noch erfasst werden.
Die Anzahl der Stichprobe soll groß sein (>20).
Berechnung des Mittelwerts  und R jeder Probe:
und R jeder Probe:
| Mittelwert der Stichproben, z.B. der 5 Teile | |
| von den 5 Teilen aus Bsp.: 1,2,3,4,5 => 5-1 = R = 4 |
Berechnung der Eingriffsgrenzen nach Vorlauf
| Prozessmittelwert: | m = Anzahl der Stichproben | |
| mittlere Spannweite: | ||
| Eingriffsgrenzen: | 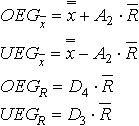 |
A2, D3 und D4 sind statisch berechnete Werte, mit einer Sicherheit von 99,37% (± 3s). Sie können aus Tabellen entnommen werden, Sie sind abhängig von der Anzahl der Stichproben! Steht oft auf Regelkarte! (Kommen von der Gaußschen Normalverteilung) |
Regelkarte
Interpretation der Spannwertkarte
-
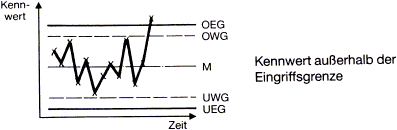
Punkt außerhalb der Eingriffsgrenze
Annahme: Systematischer Fehler liegt vor Aktion: Sofortige Untersuchung des Prozesses -
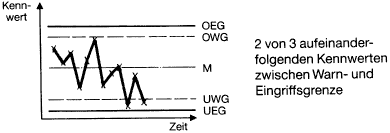
Spezielle Kurvenverläufe innerhalb der Eingriffsgrenzen
R steigt -> Streuung nimmt zu
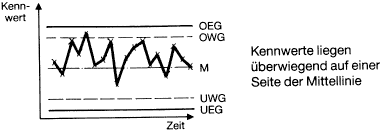
R abnehmend -> Streuung nimmt abAktion: 7 Punkte nacheinander auf einer Seite des Mittelwertes 7 Punkte, die ein stetig steigendes Intervall bilden
Abstand der Punkte von 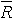
- 2/3 im mittleren Drittel des Bereichs zwischen den Eingriffsgrenzen
- 1/3 in den äußeren Bereichen
wenn nicht
- Eingriffsgrenzen falsch berechnet
- Meßwert von unterschiedlichen Fertigungslinien
- Datenmanipulation
Im Fall einer Neuberechnung der Prozeßfähigkeit nach Auffinden bzw. Ausschalten von systematischen Fehlern müssen die Eingriffsgrenzen auch neu berechnet werden.
Analyse der Mittelwerte:
Eingreifen wenn:
- Punkte außerhalb der Eingriffgrenzen
- Spezielle Kurvenverläufe innerhalb der Eingriffgrenzen (7-Punkte-Regel d.h. wenn 7 Punkte in einer Bandbreite <1/3 der Bandbreite OEG-UEG liegen)
Mögliche Ursachen:
- Prozeßmittelwert ändert sich
- Meßsystem hat sich geändert
- Eingriffsgrenzen falsch berechnet
- Stichproben enthalten Meßwerte von 2 unterschiedlichen Fertigungslinien
- Daten sind geschönt worden
Konstanten für die Berechnung der Eingriffgrenzen
| n | A2 | d2 | D3 | D4 | A3 | c4 | B3 | B4 | |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 1,880 | 1,128 | - | 3,267 | 2,659 | 0,7979 | - | 3,267 | 1,880 |
| 3 | 1,023 | 1,693 | - | 2,574 | 1,954 | 0,8862 | - | 2,568 | 1,187 |
| 4 | 0,729 | 2,059 | - | 2,282 | 1,628 | 0,9213 | - | 2,266 | 0,796 |
| 5 | 0,577 | 2,326 | - | 2,114 | 1,427 | 0,9400 | - | 2,089 | 0,691 |
|   | |||||||||
| 6 | 0,483 | 2,534 | - | 2,004 | 1,287 | 0,9515 | 0,030 | 1,970 | 0,548 |
| 7 | 0,419 | 2,704 | 0,076 | 1,924 | 1,182 | 0,9594 | 0,118 | 1,882 | 0,508 |
| 8 | 0,373 | 2,847 | 0,136 | 1,864 | 1,099 | 0,9650 | 0,185 | 1,815 | 0,433 |
| 9 | 0,337 | 2,970 | 0,184 | 1,816 | 1,032 | 0,9693 | 0,239 | 1,761 | 0,412 |
| 10 | 0,308 | 3,078 | 0,223 | 1,777 | 0,975 | 0,9727 | 0,284 | 1,716 | 0,362 |
|   | |||||||||
| 11 | 0,285 | 3,173 | 0,256 | 1,744 | 0,927 | 0,9754 | 0,321 | 1,679 | - |
| 12 | 0,266 | 3,258 | 0,283 | 1,717 | 0,886 | 0,9776 | 0,354 | 1,646 | - |
| 13 | 0,249 | 3,336 | 0,307 | 1,693 | 0,850 | 0,9794 | 0,382 | 1,618 | - |
| 14 | 0,235 | 3,407 | 0,328 | 1,672 | 0,817 | 0,9810 | 0,406 | 1,594 | - |
| 15 | 0,223 | 3,472 | 0,347 | 1,653 | 0,789 | 0,9823 | 0,428 | 1,572 | - |
|   | |||||||||
| 16 | 0,212 | 3,532 | 0,363 | 1,637 | 0,763 | 0,9835 | 0,448 | 1552 | - |
| 17 | 0,203 | 3,588 | 0,378 | 1,622 | 0,739 | 0,9845 | 0,466 | 1,534 | - |
| 18 | 0,194 | 3,640 | 0,391 | 1,608 | 0,718 | 0,9854 | 0,482 | 1,518 | - |
| 19 | 0,187 | 3,689 | 0,403 | 1,597 | 0,698 | 0,9862 | 0,497 | 1,503 | - |
| 20 | 0,180 | 3,735 | 0,415 | 1,585 | 0,680 | 0,9869 | 0,510 | 1,490 | - |
|   | |||||||||
| 21 | 0,173 | 3,778 | 0,425 | 1,575 | 0,663 | 0,9876 | 0,523 | 1,477 | - |
| 22 | 0,167 | 3,819 | 0,434 | 1,566 | 0,647 | 0,9882 | 0,534 | 1,466 | - |
| 23 | 0,162 | 3,858 | 0,443 | 1,557 | 0,633 | 0,9887 | 0,545 | 1,455 | - |
| 24 | 0,157 | 3,895 | 0,451 | 1,548 | 0,619 | 0,9892 | 0,555 | 1,445 | - |
| 25 | 0,153 | 3,931 | 0,459 | 1,541 | 0,606 | 0,9896 | 0,565 | 1,435 | - |
Interpretation der QRK:
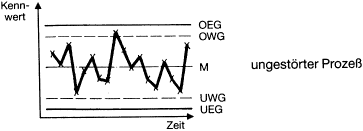
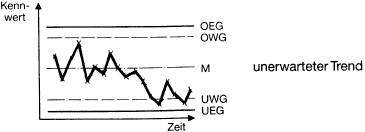
Prozeß mit systematischer Mittelwertänderung:
Beispiel:
- Werkzeugverschleiß
- Temperaturerhöhung vom Kühlmedium
Berechnung der beobachten Mittelwertes:
| => |
|
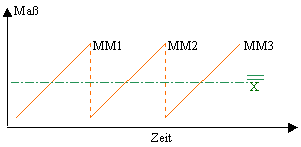
| Moving Mean: |
Über die letzten 3 Werkzeugzyklen definieren wir einen AMM (Average Moving Mean)
 |
|
| Berechnung der Grenzen: | 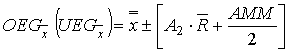 |
| Berechnung: | => |
 /s - Karten:
/s - Karten:
Berechnung der Stichprobenstandardabweichung
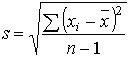
Berechnung der Eingriffgrenzen
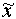 /R - Karten:
/R - Karten:
Berechnung der Eingriffgrenzen
| ungerader Sichprobenumfang: | |
| gerader Stichprobenumfang: |
