1.6 Nicht-normalverteile Merkmale
1.6.1 Gründe für Nicht-Normalität
- Die Verteilung der Merkmale unterliegt anderen statischen Gesetzmäßigkeiten als denen der Normalverteilung, z.B. Schlag, Unrundheit oder anderen null-begrenzte Merkmale ergeben häufig eine schiefe Verteilung.
- Die Verteilung der Merkmale ist komplex und kann durch keine Standard-Verteilung angenährt werden.
Zum Beispiel:
- Ein integrierter Abschaltmechanismus oder die Selbstnachstellung einer Maschine werden in den meisten Fällen nicht-normale Verteilung erzeugen.
- Produkte, die in mehreren Prozeßschritten hergestellt werden oder von mehreren ähnlichen Maschinen stammen, können nicht-normal verteilt sein, auch wenn die Produkte der einzelnen Maschine normal verteilt sind.
- Ein Trend des Mittelwertes, der beispielsweise durch Werkzeugverschleiß hervorgerufen wird, kann eine nicht-normale Verteilung verursachen.
- Auch wenn die eigentliche Verteilung der Produkte einer Maschine normal ist, können systematische Einflüsse eine nicht-normale Verteilung verursachen.
1.6.2 Das Standard-Normalverteilungsnetz
Das Standard-Normalverteilungsnetz, das auf dem Maschinefähigkeitsarbeitsblatt verwendet wird, kann auch als Mittel zur Feststellung von Abweichungen von der Normalverteilung dienen.
Wenn die Punkte ein unregelmäßiges Streubild annehmen, könnten verschiedene Interpretationen über das Verhalten der Merkmale gemacht werden. Beispiele sind (A), (B) und (C) gegenüber gezeigt. (C) zeigt zwei gemischte Normalverteilungen. Die beiden Verteilungen sollten getrennt untersucht werden.
Wenn die Punkte eine Kurve bilden, wie in (D) gezeigt, weist das darauf hin, daß das Merkmal einer regelmäßigen Nicht-Normalverteilung folgt.
Die Interpretation der Krümmung bestimmt die Wahl eines alternativen Wahrscheinlichkeitsnetzes.
Ähnlich dem Normalwahrscheinlichkeitsnetz gibt es Netze für andere Arten von Verteilungen, z.B. das logarithmische Normalverteilungsnetz oder das Weibull-Netz.
Die Punkte werden auf diesen Wahrscheinlichkeitsnetzen ähnlich eingetragen wie auf dem Netz für normalverteilte Meßwerte. Das Netz, das die beste Annäherung der eingetragenen Punkte durch eine Gerade ermöglicht, sollte für die Ermittlung der Fähigkeit verwandt werden.
Die Fähigkeitsindexe werden für null-begrenzte Merkmale mit einer oberen Spezifikationsgrenze (z.B. Schalg, Unwucht, u.ä.) wie folgt berechnet.
![]()
![]()
Für Merkmale mit nur einer unteren Spzeifikationsgrenze (z.B. Mindestfestigkeit von Stählen, Mindestreibwert von Bremsbelägen) kann nur ![]() bzw.
bzw. ![]() berechnet werden.
berechnet werden.
1.6.3 Grafische Analyse mit dem Wahrscheinlichkeitsnetz
| An den Spez. Grenzen ausgesucht; Ausschluss und Nacharbeit 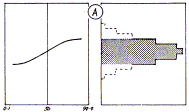 |
An einer Grenze ausgesucht 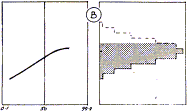 |
Mischverteilung 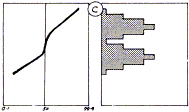 |
Schiefe Verteilung 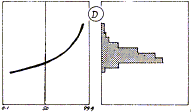 |
| Tranformation verschiedener Kurven in Geraden mit alternativen Wahrscheinlichkeitsnetzen 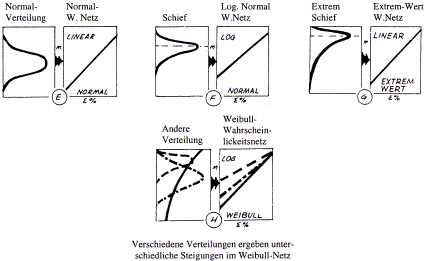 |
|
